香农采样定理内容(香农采样定理和奈奎斯特定理区别)
信号传输
两次工业革命分别使人类进入蒸汽时代和电气时代,第三次科技革命使人类进入信息化时代,虽然第四次科技革命被认为是智能时代,但是以当前的智能算法水平,基本还是停留在信息时代当中。而信息化的根基就是数据的传输。

以ISO/OSI七层网络协议为例,物理层是单纯的在物理线路上进行信息传递,比如A和B通过双绞线、同轴电缆或光纤等介质传输。传输信号假定为数字信号方波,1为高电平,0为低电平。
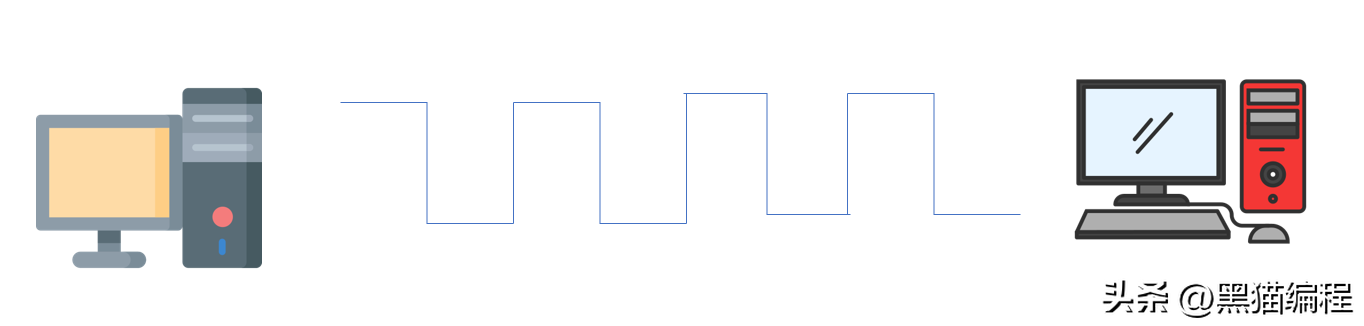
10101010
如图所示波形,代表数据10101010,每一个1或0都代表一个码元,码元可以用二进制表示,也可以用多进制表示。
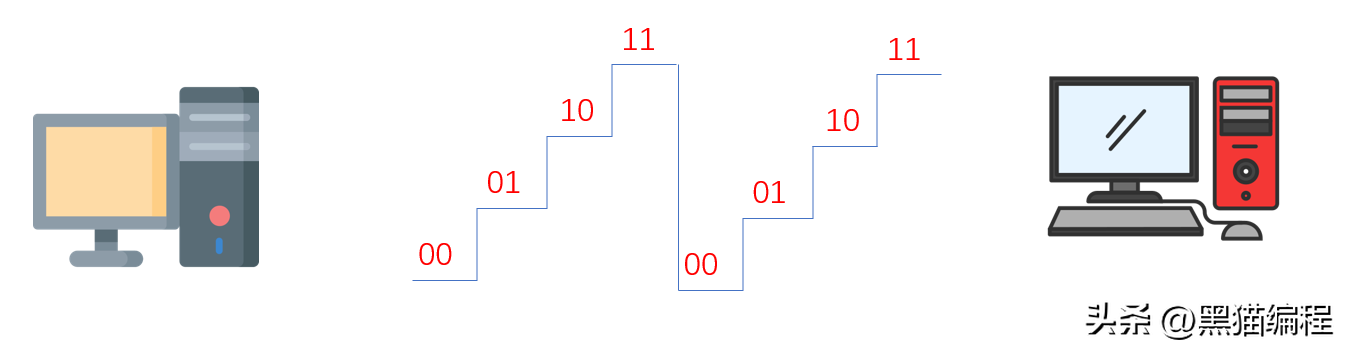
上述波形有4种状态,也就是4进制码元,每一个码元需要携带两个位信息,每个位都有0、1两种状态,因此
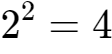
。00、01、10、11分别对应四进制0、1、2、3。
波特率和比特率
波特率是每秒传输的码元个数,单位是Baud波特。比如1s传输8个码元,那么波特率就是8B。
比特率也叫做信息传输速率,表示单位时间内传输二进制码元个数,即比特数,单位是bit/s。
由于二进制码元每个码元只需携带1个比特信息,所以波特率和比特率是相等的。但是,为了提高通信效率,我们希望尽可能多的让一个码元携带更多信息。比如,波形有16种变化,那么一个码元就需要携带
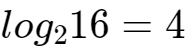
bit。

奈奎斯特定理
A到B之间进行信号传输,为了让通信效率更高,在码元相同情况下,我们可以提高1个码元携带的信息量。在码元携带信息量相同情况下,即信号进制相同,我们可以提高码元数量。但是码元数量不能无限制增加,比如1s传递10000个码元肯定比1s传递100个码元携带信息多,然而码元越多证明信号频率越高,接收端在接收时就可能会识别有误,造成信息丢失。
比如,同声传译,你的中文被实时翻译为英文,当语速较慢时,翻译过程失误率较低,如果语速较快,翻译就很难反应过来。

因此奈奎斯特就给出了定理:
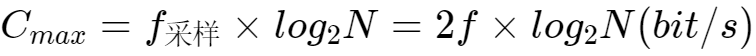
采样定理:f为原始信号最大频率,即最高频率与最低频率之差,采样频率必须大于等于最大频率的2倍,这是一个结论。
其中,N是每个码元携带的离散电平数。理论上可以无限大,实际上不可能实现,需要在无噪声环境下。
这样,就界定了最大频率范围,信号中大于最大频率的高频通量就会被拦截,因此,信号接收时是不完整的,这就造成了码间串扰现象。奈奎斯特定理的前提条件是采样定理和无噪声情况下。
香农定理
香农,作为信息论之父,奠定了信息论基础。 奈奎斯特定理可知,我们可以提升信道带宽,然而在物理硬件和经济条件制约下,带宽不可以无限增加,那么N是否也可以无限增大呢?
香农给出信噪比这一概念,S/N为信号平均功率与噪声平均功率的比值。进而得出香农公式:
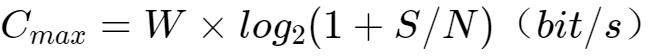
信噪比单位为(dB)也等于10
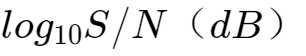
。在S/N较大时可以使用该式变形。

由此可以得出,噪声一定会存在,信号传输速率不可能无限大,给出了信号的极限传输速率。